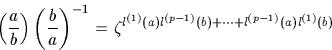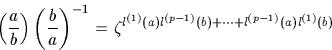Next: Réciprocité dans un corps
Up: Réciprocité et nombres premiers
Previous: Post hoc, ergo propter
Si p est un nombre premier régulier, on a :
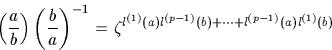
où a et b sont
dans ![${\mathbb Q}[e^{2i \pi/p}]$](img298.gif) avec
avec 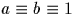 mod
mod 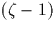
et ![$l^{(k)}(x)=[\ln^{(k)}((f(\exp(t)))]_{t=0}$](img301.gif) où f est un polynôme
de degré p-1 vérifiant
où f est un polynôme
de degré p-1 vérifiant 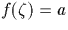 et f(1)=1.
et f(1)=1.
Cyril Banderier
7/23/1997