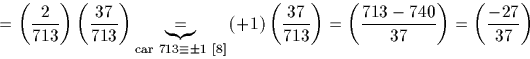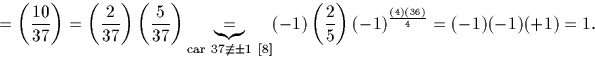Application

713 est-il un carré modulo le premier 1009 ? En utilisant la loi de réciprocité quadratique et le calcul de 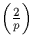$\left(\frac{2}{p}\right)$ fait au §, on a aisément :

$$\left(\frac{713}{1009}\right) =\left(\frac{1009}{713}\right)... ...}\right)=\left(\frac{8}{713}\right) \left(\frac{37}{713}\right)$$

$$=\left(\frac{2}{713}\right) \left(\frac{37}{713}\right) \un... ...t)}=\left(\frac{713-740}{37}\right)=\left(\frac{-27}{37}\right)$$

$$=\left(\frac{10}{37}\right)=\left(\frac{2}{37}\right) \left(... ... \left(\frac{2}{5}\right)(-1)^\frac{(4)(36)}{4}=(-1)(-1)(+1)=1.$$

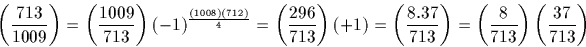
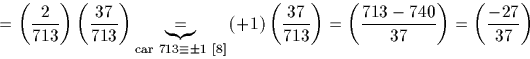
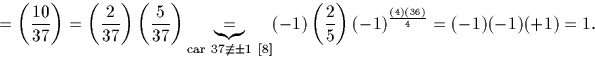
Ainsi 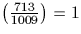$\left(\frac{713}{1009}\right)=1$ donc 713 est bien un carré modulo 1009.