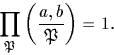
On pourra remarquer que plusieurs sujets de T.E.R., outre le nôtre, recoupent des problèmes mis en évidence par Hilbert : le quatrième sur les géométries non euclidiennes, le septième sur la transcendance de certains nombres, le dix-huitième sur les pavages (de l'espace), le vingtième sur le problème de Dirichlet...
A cette époque, une nouvelle étape dans la recherche de lois de réciprocité générales avait été franchie par Hilbert avec ses deux articles : Die Theorie der algebraischen Zahlkörper et Über die Theorie der relativquadratischen Zahlkörpern, Jahresber. Deutsch. Math., 1897 et 1899, dans lesquels il a éclairci leurs aspects locaux. Il avait établi, dans certains cas, une loi de réciprocité pour le symbole de Hilbert :
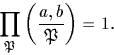
La première moitié du XXe siècle a vu diverses avancées dans
l'étude des lois de réciprocité dues à Furtwängler, Artin, Hasse et
Takagi. La loi de réciprocité dans les corps quadratiques dans le cas
général est due à [Hecke] et la forme la plus élaborée
a été obtenue par une apothéose due à I.R. Shafarevich :
A general reciprocity law, Uspekhi Mat. Nauk., 1948.
Elle est, tout comme la loi de réciprocité de Gauss, très liée à
l'étude de la décomposition d'un idéal ![]() d'un corps de nombres
algébriques
d'un corps de nombres
algébriques ![]() dans une extension algébrique
dans une extension algébrique ![]() à groupe de Galois
abélien. En particulier, la théorie des classes, qui donne la solution de
ce problème, peut être basée sur la loi de
réciprocité de Shafarevich comme l'ont fait Lapin, Cassels et [Neukirch].
à groupe de Galois
abélien. En particulier, la théorie des classes, qui donne la solution de
ce problème, peut être basée sur la loi de
réciprocité de Shafarevich comme l'ont fait Lapin, Cassels et [Neukirch].
Au jour d'aujourd'hui (redondance pléonastique voire superfétatoire ?), il reste quelques grandes conjectures offertes au monde mathématique. Gageons qu'elles figureront sur la liste des problèmes ouverts pour le XXIe siècle.
Nous citerons les suivantes, qui sont plus ou moins en rapport avec notre sujet :
- la conjecture de Riemann affirme que la fonction ![]() (une fois prolongée
analytiquement à
(une fois prolongée
analytiquement à ![]() ) ne s'annule
que sur la droite Re(z)=1/2 (à l'exception des zéros triviaux
) ne s'annule
que sur la droite Re(z)=1/2 (à l'exception des zéros triviaux ![]() ).
La conjecture de Riemann généralisée affirme la ``même chose'' pour les
L-séries de Dirichlet.
Ces dernières sont définies par
).
La conjecture de Riemann généralisée affirme la ``même chose'' pour les
L-séries de Dirichlet.
Ces dernières sont définies par
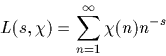
![]()
- la conjecture P ![]() NP : tout problème résoluble en temps polynomial
non déterministe est-il résoluble en temps polynomial ? C'est-à-dire : si on peut vérifier une solution en temps
polynomial, peut-on la trouver en temps polynomial ? Bien sûr,
quelque soit la réponse, il restera toujours à trouver des algorithmes de
complexité minimale pour une multitude de problèmes...On connaît
l'importance de tels progrès, et les retombées qu'ils pourraient avoir,
en cryptographie notamment, puisque cette dernière est basée sur
l'hypothèse que la factorisation ou que le logarithme modulaire sont NP.
NP : tout problème résoluble en temps polynomial
non déterministe est-il résoluble en temps polynomial ? C'est-à-dire : si on peut vérifier une solution en temps
polynomial, peut-on la trouver en temps polynomial ? Bien sûr,
quelque soit la réponse, il restera toujours à trouver des algorithmes de
complexité minimale pour une multitude de problèmes...On connaît
l'importance de tels progrès, et les retombées qu'ils pourraient avoir,
en cryptographie notamment, puisque cette dernière est basée sur
l'hypothèse que la factorisation ou que le logarithme modulaire sont NP.
- les mathématiciens, du moins ceux qui ne sont pas trop découragés par la réponse négative de Matijasevich au dixième problème de Hilbert (on s'est même demandé si le problème de Fermat n'était pas indécidable !), n'ont toujours pas résolu moult équations diophantiennes (Waring, Catalan).
- on ignore encore si de nombreuses familles de nombres vérifiant telle
propriété sont finies : par exemple les nombres premiers jumeaux (p,p+2),
repunits (1...1), de Mersenne (2n-1), de Fermat (22n+1),
de Cullen (![]() ), de Sophie Germain (p, 2p+1),
réguliers (voir §), de Wieferich (
), de Sophie Germain (p, 2p+1),
réguliers (voir §), de Wieferich (![]() ),
de Wilson (
),
de Wilson (![]() ) [Guy].
) [Guy].
- voici, pour finir, un problème important de la théorie des nombres :
la conjecture ABC.
Soit ![]() l'ensemble des triplets (A,B,C) d'entiers vérifiant
l'ensemble des triplets (A,B,C) d'entiers vérifiant
![]()